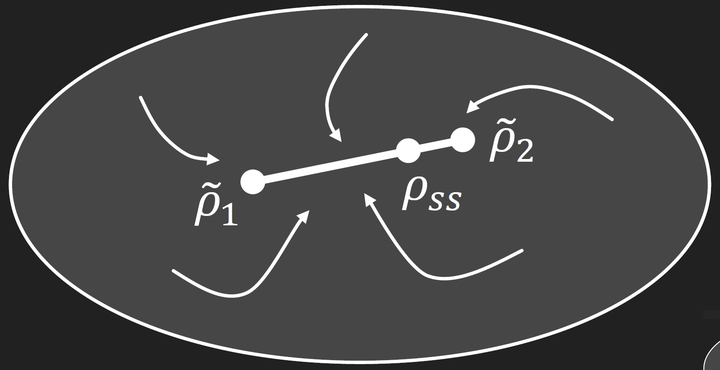
 A sketch of the flow of states on to the metastable manifold.
A sketch of the flow of states on to the metastable manifold.Abstract
We apply a recently developed theory for metastability in open quantum systems to two systems; a dissipative quantum Ising model and a quantum generalization of the East model. These exhibit strongly intermittent emission dynamics characteristic of systems with competing dynamical phases. We show that for appropriate parameters these systems dynamics display pronounced metastability, i.e., the system relaxes first to long-lived metastable states, before eventual relaxation to the true stationary state. From the spectral properties of the quantum master operator we characterise the low-dimensional manifold of metastable states for these models. We also show that the long time dynamics can be approximated by a classical stochastic dynamics between the metastable phases, directly related to the intermittent dynamics observed in quantum trajectories. In particular we demonstrate that the effective dynamics between the metastable states of the quantum East model is simply an adaption of the long-time dynamics of the classical East model.